viernes, 23 de diciembre de 2011
Feliz Navidad.
Después de haberme despedido he visto esta foto. Es de tres niñas de 4º del CEIP "Andalucía", de Cádiz. Son Alba, Elena y Alicia. Se la han hecho esta mañana. Se les ve en la cara las vacaciones por estrenar, la ilusión de la Navidad. Esta es una felicitación mejor que la que expresé en la entrada anterior. Con ella sí cierro el año.
Hace siete años publiqué un artículo sobre el espíritu navideño. Lo repito aquí,para el que tenga voluntad de
Hace siete años publiqué un artículo sobre el espíritu navideño. Lo repito aquí,para el que tenga voluntad de
Publicado por
Jaime Martínez Montero
en
23:53
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Navidad.
HASTA EL AÑO QUE VIENE.
Galia es una alumna del CEIP “Lapachar”, de Chipiona, y se tomó la molestia de resolver por escrito (y no sólo siguiéndonos en la pizarra) el ejercicio que consiste en realizar una operación de restar cuyos términos están enunciados en sus órdenes de unidades, si bien de manera poco rutinaria. Aunque ella es muy capaz y sabe identificar minuendo y sustraendo sin necesidad de trámites intermedios, y por supuesto, de resolver la operación de un vistazo, ha querido ser parsimoniosa para que todos veamos el proceso que ha seguido.
Con ella felicitamos las fiestas y despedimos el año. En Enero volveremos a abrir el blog con nuevos vídeos sobre el comienzo de la enseñanza de las ecuaciones en 2º y del empleo de la escala en la división por dos cifras en 4º, que se han quedado en el tintero por no haber tenido tiempo material de prepararlos.
Como se decía cuando yo era niño: "¡FELICES PASCUAS Y PRÓSPERO AÑO NUEVO!"
Publicado por
Jaime Martínez Montero
en
16:55
1 comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Navidad.
ARGUMENTARIO. 10
Estos inconvenientes se plantearon realmente en una sesión de claustro. En ese colegio son dos quienes trabajan el método. Una maestra no ABN interpeló a la que sí lo es con los siguientes argumentos:
10. No debería aplicarse el método de cálculo ABN porque si el resto de los maestros no lo sabe y el que sí lo aplica se pone enfermo, ¿qué se hace entonces? Además, ¿se le ha pedido permiso a la Dirección para aplicarlo?
Respecto a lo primero, casi no hay que contestar nada. Me imagino que, si nadie sabe inglés, tampoco se debe dar inglés en el colegio. Ni Educación Física, ni Música.
En cuanto a lo segundo, hay que recordar la libertad de cátedra y lo que dice la letra m) del punto 1 del artículo 7 del DECRETO 328/2010, de 13 de julio, por el que se aprueba el Reglamento Orgánico de los colegios de educación infantil y primaria: función y deber del profesorado es “la investigación, la experimentación y la mejora continua de los procesos de enseñanza correspondiente”.
El artículo 8, punto 2, letra b) señala entre los derechos del maestro el de “emplear los métodos de enseñanza y aprendizaje que considere más adecuados al nivel de desarrollo, aptitudes y capacidades del alumnado, de conformidad con lo establecido en el proyecto educativo del centro”. Naturalmente, el proyecto educativo del centro no dice por ningún lado que se prohíbe el método ABN.
Publicado por
Jaime Martínez Montero
en
16:47
1 comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Preguntas y respuestas sobre los algoritmos ABN.
martes, 20 de diciembre de 2011
Reconocimiento de números descompuestos
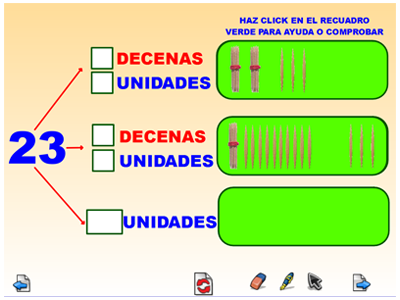
Se trata de un rotafolios para trabajar el reconocimiento de números descompuestos en decenas y unidades de diferentes formas. Para que identifiquen el número deben pulsar sobre el(los) personaje(s) que tengan la descomposición del número propuesto. El nivel de dificultad cubre hasta el 49. Además de identificar la descomposición del número, también podemos pedirles que nos digan a qué número corresponden las otras descomposiciones que no corresponde al número que les hemos pedido.
Se trata de una forma de trabajar y motivar al alumnado en la descomposición de diversas formas del mismo número. A continuación dejo unas capturas de pantalla del rotafolios. Para descargar haz click en la imagen y a continuación se describe cómo descargarlo y ponerlo a funcionar.
CÓMO USAR Y VER EL ARCHIVO EN LA PDI:
Publicado por
José Miguel de la Rosa Sánchez
en
21:18
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Materiales y Generadores.
Numeración. Valor de posición.
En una sesión de formación, un profesor de instituto me dijo que tal vez, al trabajar con números completos, no aprovecháramos las potencialidades del valor posicional de la numeración. Tal afirmación fue bastante compartida por los restantes asistentes. Mi respuesta fue clara: ¿acaso se podrían hacer los cálculos que realizan nuestros alumnos si no manejaran muy bien los órdenes de unidades?
Publicado por
José Miguel de la Rosa Sánchez
en
17:15
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
ABN en Primaria. 4º curso.
Suma posicional
Publicado por
José Miguel de la Rosa Sánchez
en
17:11
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Adición. 4º de Primaria. Formato Posicional.
Producto posicional
David trabaja el producto posicional. Es un modelo que estamos ensayando de cara a su introducción en cursos posteriores.
Yoel practica el producto posicional en un caso más complejo que el anterior.
Publicado por
José Miguel de la Rosa Sánchez
en
17:09
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Producto. 4º de Primaria. Formato Posicional.
División posicional
La división posicional es otro modelo de algoritmo que estamos valorando para su utilización en cursos posteriores.
Publicado por
José Miguel de la Rosa Sánchez
en
17:07
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
División. 4º de Primaria. Formato Posicional.
Empezando con las ecuaciones en 3º
El curso pasado ensayamos en el 3º del CEIP “Andalucía” cómo podían los niños resolver ecuaciones de primer grado. Adquirieron cierta maestría cinco niños, de los siete que elegimos para el experimento. En este curso queremos generalizar a toda la clase esta habilidad, y en los cursos 2º y 3º. Los primeros ensayos en el 3º del CEIP “San Rafael”, de Cádiz, son muy alentadores. Hasta ahora trabajamos con una sola incógnita y en uno de los términos, pero ya avanzaremos. Gara resuelve una ecuación y nos cuenta cómo lo hace. Ilustraremos cada uno de los pasos.
Publicado por
Jaime Martínez Montero
en
17:04
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Álgebra. 3º de Primaria.
Numeración en cualquier base.
Repasamos lo que ya sabían hacer en el curso pasado. Christian muestra sus habilidades.
Publicado por
José Miguel de la Rosa Sánchez
en
16:27
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Numeración en cualquier base. 4º de Primaria.
Ecuaciones de primer grado en 4º
Hemos repasado las ecuaciones que ya aprendieron a resolver algunos niños y niñas el curso anterior. En este vídeo, Óscar no ha olvidado los conceptos.
Publicado por
José Miguel de la Rosa Sánchez
en
16:25
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Álgebra. 4º de Primaria.
sábado, 17 de diciembre de 2011
ARGUMENTARIO. 9
9. Es contraproducente que niños y niñas que se han iniciado con el cálculo tradicional o lleven dos o tres cursos con esa metodología, de pronto se cambien a una muy distinta.
Este argumento toma como base el modelo de los tratamientos médicos que pueden ser incompatibles entre sí o que, con su cambio, originan efectos secundarios perjudiciales de cierta intensidad. Pues tenemos que decir que no es cierto, que tal cosa no ocurre. Que no se da ninguna contradicción.
Hemos conocido y lidiado con todas las circunstancias: se ha inciado el método en 2º, en 3º, en 4º, en 5º y hasta en 6º. En este último caso, bien es verdad, como taller complementario. No solamente eso. Todos los cursos se incorporan niños que hasta ese momento sólo habían trabajado el método tradicional. Este mismo curso, y en los colegios que visito actualmente, nos ha sucedido en 3º, 4º y 5º. Ha habido una adaptación rapidísima y los niños están encantados con la nueva forma de trabajar.
Insistimos: es que con nuestro método los niños hacen lo mismo que hacían antes, pero de una forma más comprensiva y atractiva. El niño suma, resta, multiplica, divide y hace problemas. Lo que ahora ocurre es que entiende lo que hace. Y no es mejor que se practiquen rutinas sin sentido que éstas se enmarquen en una actividad que el niño entiende.
Publicado por
Jaime Martínez Montero
en
12:27
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Preguntas y respuestas sobre los algoritmos ABN.
Pequeño reportaje del acto de presentación del nuevo libro.
El pasado jueves 15 de Diciembre, en un acto muy entrañable, se llevó a cabo la presentación del libro “Desarrollo y mejora de la inteligencia matemática en la Educación Infantil”. Hubo muchas “bajas” respecto a lo previsto. El Consejero de Educación no pudo asistir por urgencias sobrevenidas. Y por circunstancias personales ligadas a la enfermedad tampoco pudieron acudir la Inspectora General y la Jefa de Ediciones de la Editorial, que tradicionalmente nos ha acompañado. Asistieron alrededor de ochenta personas, muchas de las cuales fueron maestras (y algún maestro) comprometidas con el método ABN.
La mesa estaba constituida, de izquierda a derecha, por los autores (Jaime Martínez Montero y Concha Sánchez Cortés), la Inspectora Central de Educación de la Junta de Andalucía, María Ángeles Almirón, el Inspector Central del Ministerio de Educación y Ciencia, Francisco Medina Rivilla, y el Inspector-Jefe de Cádiz, José María González.
El Inspector-Jefe de Educación de Cádiz, José María González, presenta a los componentes de la mesa y explica el sentido del acto.
Don Francisco Medina Rivilla, en un momento de su intervención.
Doña María Ángeles Almirón, que traía la representación de la Inspectora General.
El coautor del libro, Jaime Martínez, en un momento de su intervención.
La otra autora, Concha Sánchez, sigue con interés las exposiciones.
Gesto de complicidad entre los autores durante la exposición.
Publicado por
Jaime Martínez Montero
en
11:43
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Noticias.
viernes, 16 de diciembre de 2011
Descomposición con la PDI
Con el siguiente rotafolios para la Pizarra Digital añado una herramienta de apoyo en la comprensión de la descomposición en decenas y unidades, para trabajar junto a las fichas de numeración que estoy publicando en el blog.
Lo más normal en los libros de texto es descomponer un número exclusivamente en decenas y unidades (23 en 2 decenas y 3 unidades) y cómo máxima descomposición indicar las unidades que corresponden a dichas decenas (en el ejemplo 2 decenas son 20 unidades). Sin embargo con este tipo de ejercicios queremos profundizar áun más en el dominio de la descomposición numérica, lo cual les proporcionará una mayor capacidad en el cálculo posterior. En el ejemplo anterior 23 podemos descomponerlo en 2 d y 3 u, en 1 d y 13 u, y en 23 unidades (estas 23 unidades vista como tales, cuya agrupación generará decenas), lo cual irá ampliándose en con números mayores.
CÓMO USAR Y VER EL ARCHIVO EN LA PDI:
Publicado por
José Miguel de la Rosa Sánchez
en
7:33
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Materiales y Generadores.
Decoración de números
Actualización: 5ª decena
Números para decorar la clase mientras aprenden la numeración, ilustrados con palillos formando unidades y decenas, coloreando las unidades de azul y las decenas de rojo. Útil sobre todo para introducir los números mediante el algoritmo ABN con apoyo de palillos.
Archivo con la 5ª decena, desde el 40 al 49.

Más a continuación...
Publicado por
José Miguel de la Rosa Sánchez
en
7:20
2
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Materiales y Generadores.
jueves, 15 de diciembre de 2011
El método matemático ABN será un proyecto piloto en Andalucía.
Publicado por
Jaime Martínez Montero
en
18:26
1 comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Noticias.
martes, 13 de diciembre de 2011
ARGUMENTARIO. 8
8. Los niños ABN, en un curso posterior, dentro del mismo colegio, pueden ser alumnos de un maestro o maestra que sólo trabaje con el método tradicional.
¿Y qué? Ya hemos tenido varios casos. ¿Qué les ha ocurrido a los niños que habían trabajado ABN cuando los han vuelto a sumergir en el cálculo tradicional? Pues que poco a poco han ido perdiendo habilidades de cálculo y han empeorado notablemente en su nivel de conceptualización y en su capacidad de resolución de problemas. Sí. Es una auténtica pena que se vuelva a tratamientos que empeoren la salud del enfermo, debido a que el señor médico no quiere tomarse ninguna molestia.
Pero, ¿y los alumnos? Muy bien. Acostumbrados a hacer cálculos muy difíciles, se encuentran con que lo más complicado que tienen que realizar es combinar un par de números. Así que hacen las viejas cuentas muy deprisa y muy bien: cada vez más rápido y cada vez sabiendo menos.
Como ya he denunciado en varias ocasiones, se plantea esta pregunta o se expresa este argumento como normal, cuando debería utilizarse el contrario: ¿cómo es posible que a un grupo de alumnos que han alcanzado en cálculo un nivel superior al de sus compañeros les cambien el método por otro peor, e incluso defiendan que para qué utilizar el que obtiene buenos resultados si al final va a terminar haciendo más cuentas que un tonto?
Publicado por
Jaime Martínez Montero
en
17:10
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Preguntas y respuestas sobre los algoritmos ABN.
lunes, 12 de diciembre de 2011
Noticia sobre el acto de presentación del nuevo libro.
Según me han comunicado esta tarde, el Consejero de Educación no va a poder asistir al acto debido a problemas de agenda surgidos con posterioridad al anuncio de su participación en el mismo. Por tanto, las intervenciones serán las que se anuncian en la tarjeta de invitación.
Incluimos aquí la noticia de su asistencia, así que también hay que dar la del cambio de planes.
Incluimos aquí la noticia de su asistencia, así que también hay que dar la del cambio de planes.
Publicado por
Jaime Martínez Montero
en
23:16
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Noticias.
lunes, 5 de diciembre de 2011
Multiplicación Oral.
Juan Marcos tiene una gran memoria de trabajo y mucha capacidad de cálculo. Además, explica muy bien lo que hace. Estrenamos con él los vídeos de 3º de Primaria del CEIP "Andalucía", de Cádiz.
Publicado por
José Miguel de la Rosa Sánchez
en
22:59
6
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Producto. 3º de Primaria. Formato oral.
MIR docente
Traigo al blog, como es costumbre, los artículos de opinión que de vez en cuando publico en la cadena de periódicos Joly. Este va sobre la formación y selección de docentes.
Publicado por
Jaime Martínez Montero
en
22:56
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Artículos.
domingo, 4 de diciembre de 2011
El blog supera las cien mil visitas.
Es una cifra mágica: 100.000. El canal de Youtube de AlgoritmosABN ha superado las 177.000 visitas. El "Tutor ABN" cuenta con más de mil usuarios fijos y ha sido visitado por cerca de 30.000.
Seguimos creciendo.
Seguimos creciendo.
Publicado por
Jaime Martínez Montero
en
23:21
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Noticias.
Trabajando la numeración con palillos
La maestra Mª Carmen, desde CEIP Pinar Prados ( Pozuelo ) en Madrid, nos envía unas fotografías en las que se observa cómo trabajan la numeración con palillos hasta el 15. Nos comenta que lo ha hecho como Concha Cantero, del CEIP "Reggio" de ^Puerto Real, nos muestras en uno de los vídeos del blog.
Usa una alfómbra de goma espuma para poder mantener los palillos de pié. También, como se observa en las fotografías, trabaja la numeración con palitos de chupachups.
Usa una alfómbra de goma espuma para poder mantener los palillos de pié. También, como se observa en las fotografías, trabaja la numeración con palitos de chupachups.
Publicado por
Jaime Martínez Montero
en
13:28
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
ABN en Primaria. 1º curso.
sábado, 3 de diciembre de 2011
Complementos del 10
Los complementos del 10 son aquellos números que su adición nos da la decena. En clase les podemos llamar los amigos del 10 para hacer el vocabulario más entendible a nuestro pequeño alumnado. Su aprendizaje y uso es importantísimo porque son la antesala de la suma y la resta. Dominarlos con agilidad nos facilitará la introducción al algoritmo ABN de ambas operaciones.
En este vídeo os dejamos una actividad lúdica en la cual trabajamos dichos números y además la numeración de dos en dos. También dejamos unas fotografías explicadas de la actividad y una plantilla para anotar los resultado.
IMÁGENES:
Publicado por
José Miguel de la Rosa Sánchez
en
13:06
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
ABN en Primaria. 1º curso.
Acto de presentación del nuevo libro.
Pues la cita tendrá lugar el jueves 15 de Diciembre, a las ocho de la tarde, en la sede de la Asociación de la Prensa de Cádiz. El acto es abierto y, por tanto, la entrada es libre.
El Consejero de Educación de la Junta de Andalucía ha anunciado su propósito de asistir y presentar personalmente el libro. Esta noticia la hemos sabido con posterioridad a la impresión de las tarjetas de invitación. Por ello, y si urgencias de última hora no le impidieran estar presente, las intervenciones del acto experimentarían el consiguiente cambio.
Publicado por
Jaime Martínez Montero
en
10:42
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Noticias.
ARGUMENTARIO.7.
7. Las Pruebas de Diagnóstico, Escala u otros exámenes externos están diseñadas para el cálculo tradicional, y no para el ABN.
Este argumento se desmonta en muy pocas líneas. Se ha hablado ya con la Agencia de Evaluación y en las Pruebas de Diagnóstico y Escala, que se celebrarán en Mayo, se dejará espacio en los cuadernillos para que los alumnos puedan emplear en la resolución de los cálculos el método ABN, si es que es ese el que están manejando en su clase.
Publicado por
Jaime Martínez Montero
en
10:34
2
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Preguntas y respuestas sobre los algoritmos ABN.
ARGUMENTARIO.6.
6. Los libros de texto desarrollan el método tradicional.
¿Y qué? ¿No se puede salir de ellos? ¿Se es maestro o maestra, o jornaleros del libro de texto? El libro de texto es una pieza más, una ayuda más para el profesor, pero no es lo único. Si algún docente piensa que su trabajo consiste exclusivamente en “dar” el libro, entonces que no se acerque al método ABN hasta que no haya libros que lo incluyan.
En los cientos de clases en que se trabaja el método ABN los libros de texto no son ni excusa ni impedimento. En el caso del Primer Ciclo, porque se puede escribir en ellos, y los niños, allí, pueden escribir sus formatos y realizar sus operaciones. En otras entradas del blog mostramos fotos de libros adaptados en 1º de Primaria. Pero ni esto hace falta. El niño hace la operación en su cuaderno y traslada el resultado al libro. En el caso del 2º y 3º Ciclo el problema es todavía menor. No se puede escribir en ellos, por lo que el alumnado resuelve las operaciones directamente en su cuaderno. Y santas pascuas.
Por otro lado, el libro de texto de matemáticas no sólo trae cálculo, sino medidas, estadística, estimaciones, azar, geometría, etc. Es decir, que buena parte de su contenido no es afectado por el desarrollo del método.
Otra cosa, no expresada, es que la aplicación del método requiera del docente ir algo más allá de lo prescrito en el texto, porque su contenido lo supera el niño, o porque haya que introducir algún aspecto no contemplado. Pero eso entra dentro del oficio.
Publicado por
Jaime Martínez Montero
en
10:33
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Preguntas y respuestas sobre los algoritmos ABN.
martes, 29 de noviembre de 2011
Noticias
ESCUELA DE PADRES
VIERNES 25 DE NOVIEMBRE
¿Estas interesado/a en conocer el nuevo sistema de CÁLCULO EN ABN?
PODRAS AYUDAR A TUS HIJOS EN SUS TAREAS DE MATEMÁTICAS
ASISTE ESTE VIERNES DE 9 A 10 EN EL COMEDOR
CEIP MAESTRO MANUEL APARCERO CURSO 2011-12
El Director del CEIP "Manuel Aparcero" de Chipiona, me hace llegar su cartel anunciador de una sesión informativasobre el ABN dedicada a los padres de su colegio.
Me envía la noticia porque va en la línea de lo que hemos señalado en uno de los argumentarios: la necesidad de explicarle a los padres y madres del alumnado lo que se va a hacer para que les parezca bien, lo entiendan y puedan ayudar a sus hijos.
Publicado por
Jaime Martínez Montero
en
19:47
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Noticias.
domingo, 27 de noviembre de 2011
Multiplicación por dos cifras en 2º de Primaria
No deben ver este vídeo como pretencioso, sino como una forma inteligente de que los niños repasen las tablas que están aprendiendo y, a la vez, practiquen la suma. Como se trata de chicos muy pequeños, desdoblan el multiplicador y, en realidad, lo que hacen es desarrollar cálculos sucesivos. Sin embargo, no nos resistimos a someter al bueno de Fran, que se tiene que subir en un banco para llegar bien a la pizarra, a unas cuantas preguntas, con el fin de comprobar si entiende el sentido del algoritmo y tiene el control de lo que hace.
Publicado por
José Miguel de la Rosa Sánchez
en
20:28
1 comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Producto. 2º de Primaria.
Preguntas envenenadas.
Una de las señas de identidad del método ABN es la formulación de preguntas sobre los algoritmos que han realizado los chicos o chicas. Con ello se pretende averiguar si sólo ha habido resolución mecánica o, por el contrario, si se ha controlado el proceso y se sabe dar cuenta de él. La dificultad de las preguntas se puede graduar, pero las que recogemos en este vídeo son de las más difíciles. De hecho, se pregunta por la operación contraria a la que han realizado.
Publicado por
José Miguel de la Rosa Sánchez
en
20:17
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Producto. 3º de Primaria.
sábado, 26 de noviembre de 2011
Generador de operaciones ABN
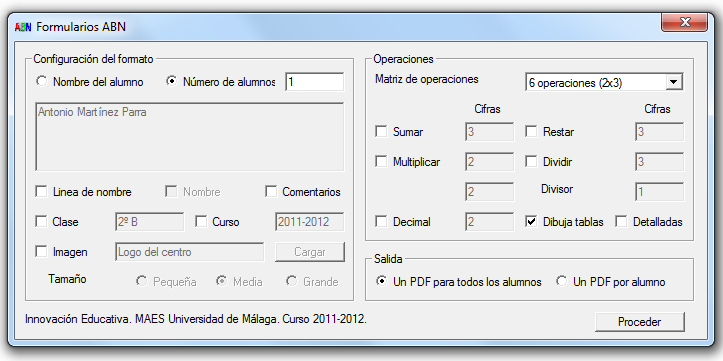
Los que trabajamos el algoritmo ABN contamos con una nueva herramienta muy completa para generar operaciones para este tipo de cálculo. Se trata de una nueva aplicación realizada por ENRIQUE RUIZ, profesor de secundaria de Almería. Una nueva colaboración de alguien que se siente atraído por nuestra forma de trabajar el cálculo.
Se trata de un generador de ejercicios en pdf muy completo, sencillo, que puedes descargar y ejecutar desde tu ordenador y con las opciones justas para crear las actividades que creamos oportunas. Podemos elegir cualquiera de las cuatro operaciones básicas, con o sin decimales, crear ejercicios personalizados con nombre y apellidos, incluir una imagen (añadiéndola desde nuestro ordenador) que haga más atractiva la ficha para el alumno, definir qué tipo de línea quiero para las operaciones (típicas del cálculo ABN) y la cantidad de operaciones hasta un máximo de 12 por ficha, en columnas de tres.
A continuación un ejemplo de ficha generada
Publicado por
Jaime Martínez Montero
en
13:37
6
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Materiales y Generadores.
viernes, 25 de noviembre de 2011
EL ÍNDICE DEL NUEVO LIBRO.
Nos han solicitado bastantes docentes que incluyamos el índice del nuevo libro ("Desarrollo y mejora de la inteligencia matemática en la Educación Infantil") como una forma sencilla de que se puedan hacer alguna idea sobre el contenido. Me parece muy bien y se incluye a continuación. Es un documento largo, pues el libro consta de 17 capítulos. Pero aquí está para el que lo quiera leer.
MARTÍNEZ MONTERO, J., y SÁNCHEZ CORTÉS, C. (2011). Desarrollo y mejora de la inteligencia matemática en la Educación Infantil. Madrid: Wolters Kluwer.
ÍNDICE.
CAPÍTULO I. INTRODUCCIÓN .................................................................. 17
1. LAS MATEMÁTICAS RODEAN A LOS NIÑOS .................................... 19
Publicado por
Jaime Martínez Montero
en
17:48
17
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
ABN en Infantil.
ARGUMENTARIO.5.
5. El niño que llega nuevo a la clase se encuentra perdido. El que tenga que cambiar de colegio tendrá muchas dificultades porque irá a un lugar donde se trabajará el cálculo tradicional.
De ambas situaciones tenemos bastantes experiencias. En el primer caso, cada año se reciben niños en los grupos ABN, que tardan muy poco en aprender las nuevas técnicas e integrarse. No hablamos de 1º, sino de 3º, de 4º y de 5º, que son casos que se nos han presentado en el presente curso. Uno de los últimos ha sido algo especial. Es en un 4º. La madre del niño es profesora de Secundaria de Matemáticas, y sabedora de que el grupo al que se cambiaba su hijo practicaba ABN, se lo enseñó antes. Así que llegó con bastante trabajo adelantado.
En el segundo caso los maestros que reciben a nuestros niños se ponen muy contentos. En primer lugar, porque antes de que abandonen el centro se les enseñan las cuentas de toda la vida, por lo que no han de partir de cero. En segundo lugar, porque los alumnos ABN tienen un nivel de cálculo alto y están acostumbrados a realizar combinaciones de números complicadas, por lo que no sólo no tienen dificultades, sino que hacen las operaciones muy deprisa. Jauja, vamos. Imagínense niños ABN de 2º o 3º que en sumas y en restas obtienen directamente el resultado. Llegan al centro nuevo y en lugar de calcular de una vez, por ejemplo, 146 + 358, lo que hacen es combinar 6 con 8, 5 con 4 y 3 con 1. Para ellos es una simpleza. Hacen las cuentas viejas muy deprisa. Luego, poco a poco, pagan un tributo doble: comienzan a perder sus destrezas de cálculo mental, y empeoran notablemente su capacidad de resolución de problemas. Eso sí, las cuentas las hacen volando. Ya saben que para algunos docentes esto es lo más importante del mundo.
Publicado por
Jaime Martínez Montero
en
17:30
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Preguntas y respuestas sobre los algoritmos ABN.
jueves, 24 de noviembre de 2011
UNA BUENA NOTICIA. UN NUEVO LIBRO SOBRE EL ABN EN EDUCACIÓN INFATIL.
En colaboración con Concha Sánchez, que ha trabajado 20 años en Educación Infantil, ha salido un nuevo libro. En esencia, es el comienzo del cálculo ABN en esta etapa. Ahora sí partimos de cero para entroncar con el comienzo del cálculo en Primaria.
Sólo quiero reflejar aquí la noticia. Más adelante explicaremos su contenido con más detalle.
Acaban de comunicarme su salida, y quiero darla a conocer a los muchos seguidores del blog.
Sólo quiero reflejar aquí la noticia. Más adelante explicaremos su contenido con más detalle.
Acaban de comunicarme su salida, y quiero darla a conocer a los muchos seguidores del blog.
Publicado por
Jaime Martínez Montero
en
19:13
1 comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
ABN en Infantil.
miércoles, 23 de noviembre de 2011
Ordenar de mayor a menor y viceversa
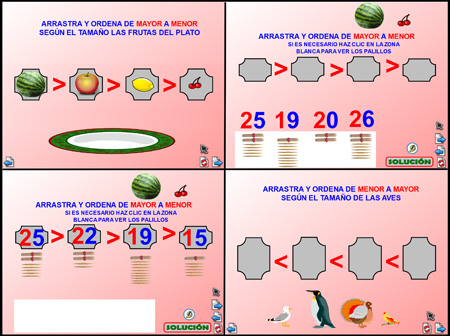
Este rotafolios, para la PDI, me ha resultado muy útil en la ejemplificación y realización de ordenación de números, ya que además de un ejemplo con imágenes, además cada serie numérica se ilustra con su correspondiente representación en decenas y unidades mediante palillos, los cuales están ocultos bajo un lienzo blanco, que podemos retirar o no a nuestro gusto, pero que una vez ordenado muestra tanto numéricamente como gráficamente la secuencia.
Aquí dejo algunas capturas de pantallas del rotafolios, para descargarlo haz clic sobre la imagen e información sobre su uso al final del artículo.
Publicado por
José Miguel de la Rosa Sánchez
en
14:45
1 comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Materiales y Generadores.
sábado, 19 de noviembre de 2011
ARGUMENTARIO.4.
4. Se pierde la ayuda de la familia, pues los padres no pueden echar una mano porque no saben cómo se hacen las nuevas cuentas.
Tenemos la suficiente experiencia para decir que esto no es cierto. Es verdad que hay que explicarle a los padres cómo son los nuevos algoritmos y solicitar su colaboración. Una vez hecho esto, son los primeros entusiastas. Por otro lado, hablamos de personas adultas que no tienen gran dificultad en aprender los nuevos
Publicado por
Jaime Martínez Montero
en
23:52
2
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Preguntas y respuestas sobre los algoritmos ABN.
Iniciación a la numeración 3
Tercera entrega. Fíjense en todo lo que hay detrás.
Publicado por
Jaime Martínez Montero
en
23:46
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
ABN en Primaria. 1º curso.
Iniciación a la numeración 2
La pregunta que más me hacen en las sesiones de formación es "¿cómo se empieza en Primero?" Pues vamos a contestar con ejemmplos de lo que hace una maestra "fundadora". Esta es la entrega número dos.
Publicado por
Jaime Martínez Montero
en
23:45
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
ABN en Primaria. 1º curso.
Fotografías del CEIP Serafina Andrade
Noticias desde el CEIP "Serafina Andrade", de Chiclana. Nos quieren mostrar parte de su trabajo.
Publicado por
Jaime Martínez Montero
en
23:42
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
ABN en Primaria. 1º curso.
Productos elementales por dos cifras. Multiplicación por 5. Cálculo mental. ¿Se puede pedir más a alumnos de 2º de Primaria?
Una nueva sorpresa desde Rota. Esto hacen los niños de 2º en el mes de Noviembre.
Publicado por
Jaime Martínez Montero
en
23:39
1 comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Producto. 2º de Primaria.
jueves, 17 de noviembre de 2011
Explicación de cómo hacen la división sintética
Ya hemos puesto algunos vídeos en los que los niños hacen la que hemos llamado "división sintética", e inclusive uno en el que un alumno la resuelve oralmente. Cristian también la hace, pero además explica cómo lo hace.
Publicado por
José Miguel de la Rosa Sánchez
en
23:17
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
División. 4º de Primaria. Formato sintético.
El vídeo del Centenario
Este vídeo es muy especial. Hace el número cien de todos los que se han ido publicando. Por eso hemos querido que lo protagonizaran Alicia y Yoel, que fueron los que hicieron los dos primeros. Aquello fue alrededor de las Navidades del 2009-2010. En la cara y en la voz se les nota el paso de los años (bueno, no llegan a dos).
También nos hemos preocupado por el contenido, porque fuera especial. Queríamos que demostrara la
Publicado por
José Miguel de la Rosa Sánchez
en
23:12
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Producto. División. 4º de Primaria. Formato sintético.
miércoles, 16 de noviembre de 2011
División Oral
Ya hemos incluido vídeos de divisiones por una cifra en las que los alumnos prescinden de los restos parciales. Concha, la maestra, me comentó que un niño (este, Andrés) le había dicho que él era capaz de resolverla sin escribir los números, oralmente. Cuando pude ir a la clase le pregunté si era verdad loque había dicho y si se atrevía a hacerlo. Me dijo que sí. ¡Y con mucha razón! Me faltó tiempo para grabarlo.
Publicado por
José Miguel de la Rosa Sánchez
en
23:46
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
División. 4º de Primaria. Formato oral.
Buscando decenas.
Es un ejercicio derivado del que se muestra en el vídeo que antecede a este. Se trata de averiguar, en este caso, cuántas decenas faltan de un número conocido que se ha descompuesto en sus órdenes de unidades, si bien no de forma rutinaria. Fran fue el primero en averiguarlo y por eso lo grabamos a él.
Publicado por
José Miguel de la Rosa Sánchez
en
23:42
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
ABN en Primaria. 4º curso.
Sustracción por ordenes de unidades.
Con Mario estrenamos una nueva forma de acercarnos a la resolución de sustracciones. Los datos se ofrecen desmenuzados en órdenes de unidades, que en ocasiones se superponen. El alumno debe "traducirlos" y, una vez hecho, efectuar la operación.
Con este tipo de operaciones intentamos ligar las destrezas de la numeración al cálculo. Lo hacemos también con la suma, de la que también pondremos algún vídeo. Nótese que se va a algo más allá de decir cómo se llama el lugar que ocupa cada una de las cifras. Vamos, que nos apartamos de lo más rutinario.
Publicado por
José Miguel de la Rosa Sánchez
en
23:32
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Sustracción. 4º de Primaria. Formato posicional.
Doble resta.
Isaiah resuelve una doble resta con acierto y mucha seguridad. Las respuestas que da a las preguntas que le hacemos al final muestran el alto dominio conceptual de la operación.
Publicado por
José Miguel de la Rosa Sánchez
en
23:29
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Doble resta. 3º de Primaria.
División mixta (abierta basada en el valor posicional).
Se trata de una división mixta. Es abierta, pero basada en el valor posicional. Propusimos este algoritmo a sugerencia de Encarni, la maestra. Este grupo comenzó con el cálculo ABN en 5º, y algunos de los alumnos han tenido dificultades con el algoritmo de la división por dos cifras. Para ellos va dirigido. Creemos que es una buena alternativa para quienes comiencen el método en cursos avanzados. En esencia sigue siendo un algoritmo abierto, de gran flexibilidad, que permite su adaptación a la capacidad de cálculo de cada alumno y alumna. Acabamos de echarlo a rodar. Ya iremos contando cómo va.
Publicado por
José Miguel de la Rosa Sánchez
en
23:19
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
División. 6º de Primaria. Formato mixto.
viernes, 11 de noviembre de 2011
Argumentario.3.
3. Cuando lleguen al Instituto, los alumnos ABN van a ir con desventaja y pueden tener serios problemas por su modo de operar.
En primer lugar, quiero distinguir entre quienes me plantean esta pregunta con ánimo de requerir una información complementaria o aclarar una duda, de los que dan por sentado que el método ABN se convierte en un obstáculo para la marcha del alumno en etapas superiores a la primaria y, por tanto, convierten esta afirmación en un elemento de descalificación del método. Estos segundos son los sujetos del presente argumentario.
A quien me hace esta afirmación le suelo responder con una primera pregunta: “¿qué instituto o
Publicado por
Jaime Martínez Montero
en
18:29
1 comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Preguntas y respuestas sobre los algoritmos ABN.
jueves, 10 de noviembre de 2011
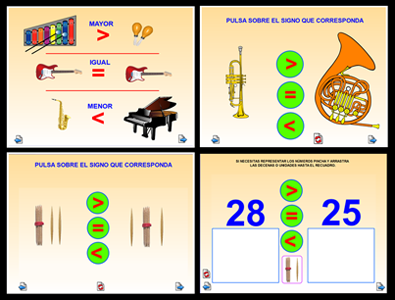
Mayor - Menor - Igual
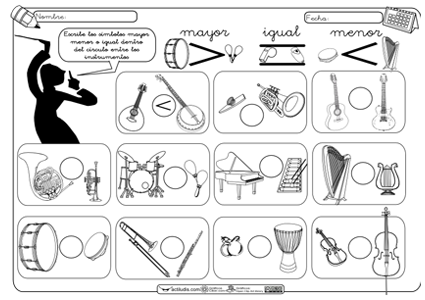
Con estas actividades se puede introducir la comprensión de los signos " >, <, =" . La primera se trata de una ficha con instrumentos musicales en los cuales la comparación es de los tamaños y la segunda se trata de un rotafolios para la PDI con el programa "Activinspire" en el que se repasa, siguiendo con los gráficos de instrumentos musicales, el significado de dichos signos matemáticos, se pasa a comparar decenas y unidades representadas mediante palillos y se termina comparando números hasta el 29, pero con la posibilidad de usar los palillos para representar dichos números como ayuda en el proceso, si fuese necesario.
ROTAFOLIOS PARA LA PDI
(Capturas del rotafolios)
Publicado por
José Miguel de la Rosa Sánchez
en
19:04
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Materiales y Generadores.
jueves, 3 de noviembre de 2011
ARGUMENTARIO.2.
2. Los cálculos ABN son mucho más lentos y requieren de mucho más tiempo.
Es una de las críticas que me han producido más perplejidad. La base de esa misma es sencilla. Para resolver una suma de dos sumandos de tres cifras cada uno, en el cálculo tradicional se emplean tres cifras, mientras que en el cálculo ABN hacen falta muchísimos más. No hablemos de la resta o la multiplicación por una cifra, en que las diferencias se acentúan.
Hay un primer argumento a emplear: la velocidad no es el objetivo decisivo. No se trata de que el alumno haga cuentas muy deprisa, sino de que haga cálculos comprendiéndolos y sabiendo lo que hace. No convirtamos el cálculo en algo parecido a la antigua “Mili” o Servicio Militar, que decían que era el lugar donde no se hacía nada, pero eso sí, muy deprisa.
Pero es que tampoco es verdad que los alumnos ABN sean más lentos. Puede que sí lo sean en algún
Publicado por
Jaime Martínez Montero
en
19:09
2
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Preguntas y respuestas sobre los algoritmos ABN.
martes, 1 de noviembre de 2011
Primeras fotos de un nuevo grupo y de un nuevo maestro. CEIP "Juan XXIII", de Puerto Real
Benito García Peinado es el tutor del grupo de 2º de Primaria del CEIP "Juan XXIII". Acaba de incorporarse al nuevo método. Este es su primer testimonio, pero estoy convencido de que no va a ser el último.
Publicado por
Jaime Martínez Montero
en
13:24
2
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
ABN en Primaria. 2º curso.
sábado, 29 de octubre de 2011
Argumentario.1.
1. LOS ALUMNOS QUE TRABAJAN EL NUEVO MÉTODO SIRVEN DE COBAYAS O CONEJILLOS DE INDIAS.
“Ninguna mujer debería tomar la píldora durante 20 años hasta que un número suficientemente grande la hubieran probado ya durante ese mismo período”. No recuerdo a quién pertenece esta frase, pero la anoté.
No. No son cobayas. Tal vez lo fueran las primeras clases. Pero ya tenemos datos, resultados, y nuestros alumnos no se someten a ninguna cura incierta ni a ninguna aventura que no se sabe cómo va a acabar. Ni mucho menos.
Pero el argumento hay que desmontarlo con un razonamiento en contrario. Lo que es una temeridad es mantener un método que lleva decenas y decenas (cientos) de años, y con millones y millones de alumnos, fracasando. Es un lugar común entre los docentes señalar que los niños hacen muy mal el cálculo mental (más allá, claro de mezclar dos dígitos) y que no saben resolver problemas. Y, digo yo, si eso es así, ¿qué modo de enseñar es ese que no consigue aquello que persigue? Por consiguiente, que quede claro que no se trata de que alumnos que gozan de unos magníficos niveles de aprendizaje abandonen un camino seguro y lo pongan todo en riesgo por iniciar una aventura incierta, sino de enmendar una situación bastante catastrófica. Mantener el método tradicional es algo peor que hacer un experimento. Al fin y a la postre, este puede salir bien. Apostar por lo de toda la vida es tener la absoluta certeza de que el alumno no sabrá calcular (aunque sepa hacer cuentas), no sabrá resolver problemas y, además, odiará ese trabajo. En definitiva, en la mayor parte de los casos obtendremos un incompetente cargado de prejuicios contra aquello que le permitiría salir de su ignorancia.
Publicado por
Jaime Martínez Montero
en
12:39
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Preguntas y respuestas sobre los algoritmos ABN.
Argumentario
En las reuniones o charlas que tengo con grupos de maestros y maestras me piden que incorpore al blog argumentos y razones que defiendan el nuevo método ABN y, sobre todo, que desmonte los que ponen en circulación aquellos que defienden el método tradicional. No es una mala idea. Me argumentan estas maestras (y algún que otro maestro) que en ocasiones el problema de la puesta en marcha de los algoritmos ABN en un centro no es la falta de voluntad o de confianza, sino la presión que ejercen compañeros y compañeras significadas del centro para que tal actuación no se desarrolle. Por eso, y aunque algunas se defienden muy bien, me dicen que no les vendrían mal algunos refuerzos.
Es verdad. Esto ocurre. Conozco al menos tres centros en los que les han quitado las ganas o les han hecho ver a los que iban a comenzar, los inconvenientes que se originarían si se metían en esa aventura. A mí estas cosas me parece lamentables e impropias de un colegio, de unos maestros y de unas personas que tienen como principal función formar a niños. No lo digo, y esto quiero dejarlo muy claro, porque me parezca mal que haya docentes que sigan con el cálculo tradicional. Allá cada uno, y sólo en España debe haber decenas de miles que trabajan de esta manera. Nosotros, insisto, jamás hacemos la mínima fuerza para atraer a nadie que no quiera, ni vamos a donde no nos llaman. Pero lo que denunciamos es otra cosa: yo no quiero cambiar mi metodología, en uso de mi libertad de cátedra, pero es que tampoco quiero que tú lo hagas. O dicho de otra forma: en uso de mi libertad de cátedra hago todo lo que puedo para que tú no la puedas ejercer... si a mí no me parece bien lo que haces.
He hecho una recopilación de tales argumentos. Como contestar a todos de una vez puede ser largo y aburrido, solo los enumeraré y poco apoco iré ocupándome de ellos. En esta primera semana contestaremos al primero:
Publicado por
Jaime Martínez Montero
en
12:34
2
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Preguntas y respuestas sobre los algoritmos ABN.
Un buen detalle.
Es un buen detalle el del grupo de maestras del "San José de Calasanz", de Rota, encabezadas por Sara Herrera.
Han tenido la buena idea de elaborar una agenda ABN, en la que a los alumnos y alumnas se les ponen las tareas para casa. Y, naturalmente, también se puede emplear en clase.
El formato es a la vez sencillo y práctico. Tiene una parte para anotaciones y luego aparecen los clásicos enrejados del método.
La Agenda permitirá seguir la evolución y progresos de los alumnos a lo largo del curso.
Finalmente, hay que señalar también la buena disposición del colegio y de su equipo directivo. Esta Agenda es una muestra más del apoyo que recibe la nueva metodología en ese centro.
Han tenido la buena idea de elaborar una agenda ABN, en la que a los alumnos y alumnas se les ponen las tareas para casa. Y, naturalmente, también se puede emplear en clase.
El formato es a la vez sencillo y práctico. Tiene una parte para anotaciones y luego aparecen los clásicos enrejados del método.
La Agenda permitirá seguir la evolución y progresos de los alumnos a lo largo del curso.
Finalmente, hay que señalar también la buena disposición del colegio y de su equipo directivo. Esta Agenda es una muestra más del apoyo que recibe la nueva metodología en ese centro.
Publicado por
Jaime Martínez Montero
en
11:02
1 comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Noticias.
sábado, 22 de octubre de 2011
Iniciación a la numeración con apoyo de la recta numérica
Las fotos que ilustran el proceso para la iniciación de la numeración en la segunda decena, son del alumnado de Primero A y B del CEIP "Alonso de Aguilar" en Aguilar de la Frontera (Córdoba).
Con esta actividad se busca como objetivo que el alumnado identifique visual y manipulativamente el concepto de decena y que traslade dicha experiencia al papel. Debajo de las fotografías se va explicando el proceso seguido.
Foto 1: Una vez que el alumnado conoce y domina la primera decena, el objetivo es lograr que entienda el concepto de decena y que lo domine para poder formar y operar con el resto números hasta el 99. El alumno representa en la recta numérica del suelo, cada número con sus correspondientes palillos, pinchándolos en la unión del número con la pieza del puzzle de goma.
Foto 2-3-4: Cuando llegamos al 10 ponemos los 10 palillos correspondientes y planteamos si podemos representar dicho número de otra forma distinta, pero siguiendo usando los palillos. No suelen tardar en darse cuenta (ya les mostramos en clase que cuando tenemos 10 los palillos los enlazamos y llamamos decena) y recordar lo que hemos trabajado en clase y cambian los 10 palillos por la decena de palillos.
Foto 5: Una vez solucionado el cambio que supone el número diez, seguimos representando el resto de números de la segunda decena.
Foto 6: En este momento hacemos una serie de reflexiones con el alumnado, para ello observamos cómo ha quedado todo y buscamos que encuentren las similitudes y diferencias en la recta representada:
- La decena de palillos se repiten en la pieza del puzzle con el número 1
- ¿Qué diferencia hay entre los palillos situados en el 1 de las unidades y el de las decenas?. ¿Es el mismo número?.
Separamos las piezas de la primera decena y las colocamos junto a las unidades de la segunda decena:
- ¿Qué tienen en común?.
- ¿En qué se diferencian ambas rectas numéricas?.
Foto 7 y 8: Realizamos representaciones en la recta numérica de la mesa de los alumnos, comprobando que han entendido el uso de las decenas.
Foto 9: Iniciamos la representación de los número fuera de la recta numérica, puede ser en una bandeja, sobre la mesa o sobre una hoja de papel. La idea es ir prescindiendo del uso de la recta numérica, aunque siga presente sobre la mesa.
Foto 10: Escribimos el número en papel que hemos representado, diferenciando mediante el color azul las unidades y de rojo las decenas. Seguimos insistiendo que las decenas de palillos es ese número rojo que ponemos en el papel.
Foto 11: Proceso inverso, escribimos el número en el papel y comprobamos que los representan mediante los palillos.
Publicado por
Jaime Martínez Montero
en
11:24
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
ABN en Primaria. 1º curso.
Descomposiciones arborescentes.
Sara Herrera, del CEIP "San José de Calasanz", de Rota, nos manda unas fotos sobre ejercicios de descomposición de sus alumnos de 2º. Casi mezclan la destreza con el arte. Nos ha mandado también un vídeo, en el que se ve no sólo lo bien que lo hacen, sino cómo lo disfrutan y la rapidez con qué operan. Desgraciadamente, la calidad de la pizarra es tan mala que no se veía lo que escribían los niños. Volveremos a grabarlos y queda pendiente su inclusión en el blog.
El ejercicio no consiste en resolver la operación, sino en descomposiciones sucesivas de sus términos.
El ejercicio no consiste en resolver la operación, sino en descomposiciones sucesivas de sus términos.
Publicado por
Jaime Martínez Montero
en
10:54
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
ABN en Primaria. 2º curso.
Iniciación a la numeración.
Un nuevo grupo ABN comienza en 1º en el CEIP "Reggio", de Puerto Real. Con el fin de ilustrar los comienzos del método en Educación Primaria vamos a seguir especialmente a este grupo. Su maestra ya es experta. Es su tercer curso y su segundo con los alumnos de 1º. Esta es la primera entrega. La finalidad del ejercicio es muy importante. Se trata de dar contenido a las grafías de los números, a qué sepan quéhay exactamente detrás de ellas.
Publicado por
Jaime Martínez Montero
en
10:44
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
ABN en Primaria. 1º curso.
lunes, 17 de octubre de 2011
Doble resta en el CEIP "San Rafael", de Cádiz.
El grupo de 3º de Primaria ha inventado un problema (y lo ha resuelto) que responde a una doble resta. Su tutor (Francisco Camero) me ha avisado de algunas de las singularidades de su resolución. Desde las técnicas de cálculo más elementales hasta las más rápidas, he aquí la sucesión de soluciones.
El alumno ha encontrado un problema lógico y realista. Sin embargo, su cálculo ha sido prudente. Primero se ha enfrentado a uno de los sustraendos y, cuando ha acabado con él, ha abordado el otro.
No tiene problemas en desdoblar o descomponer en el momento que ve alguna dificultad.
En este caso, el problema es lógico, pero poco realista dado lo económico que salen el coche y la moto.
Lo ha resuelto de una forma muy ortodoxa, utilizando, como el anterior, el método sucesivo. Acomete el primer sustraendo y lo descompone sucesivamente en centenas, decenas y unidades. Una vez que acaba con él, comienza con el segundo sustraendo, al que le aplica la misma técnica.
Esta niña propone un problema lógico, pero menos realista. Emplea el método simultáneo con alguna peculiaridad. Es capaz de reunir en un sólo sustraendo 240 del primero y 314 del segundo, y quita los 554 de una vez.
Pero no tiene seguridad a la hora de cruzar la "frontera" del 300. Por ello, quita 2 y luego 1. Ahora está en condiciones de sustraer números más complicados. Es loque hace juntando los restos de los dos sustraendos y sustrayéndolos de una vez.
No sé lo que son los Monster High, pero el problema es lógico y no puedo juzgar su grado de realismo.
La niña o el niño emplea la técnica simultánea, pero de una forma más canónica que el anterior. Primero quita todas las centenas y luego todas las decenas. Sin embargo, no se atreve a hacer lo mismo con las unidades, y las detrae sucesivamente. ¿Por qué? Pues no lo sabemos, pero les pasa a muchos.
Es lógico y realista, aunque el bosque haya tenido muy mala suerte.
Tiene una técnica buena. En el primer sustraendo recoge todas las centenas, las decenas del primer sustraendo y seis de las unidades del primero, dejando una. Con ello no se complica la vida a la hora de detraer.
Después, no se atreve a descontar veinticinco, sino que primero quita diez para redondear y luego los quince.
El problema es lógico y realista, siempre y cuando que las prendas sean de una marca de bastante lujo.
El método que emplea es el sucesivo, pero ello no es un retroceso. Ni mucho menos. Lo que hace es quitar de una vez cada uno de los sustraendos. Y ninguna de esas sustracciones es fácil.
Es admirable la capacidad de cálculo alcanzada.
Problema lógico y poco realista. Pero es que ha puesto toda su capacidad, que es muchísima, en el cálculo. Es asombroso. Se trata de un niño que está comenzando 3º de Primaria.
Emplea el método simultáneo. Pero casi sobran las palabras. Suma mentalmente 247 y 324 (571) y detrae esa cantidad de golpe, en un único intento.
Para que el lector o lectora se dé cuenta de la dificultad, puede intentar realizar esta operación del mismo modo.
En definitiva, la observación de los trabajos de los niños y niñas nos permite construir el mapa de la evolución del pensamiento matemático de los niños y las fases por las que pasan. Aprendemos mucho, especialmente que los alumnos y alumnas son capaces de hacer cosas mucho más difíciles de las que nos podemos imaginar.
El alumno ha encontrado un problema lógico y realista. Sin embargo, su cálculo ha sido prudente. Primero se ha enfrentado a uno de los sustraendos y, cuando ha acabado con él, ha abordado el otro.
No tiene problemas en desdoblar o descomponer en el momento que ve alguna dificultad.
En este caso, el problema es lógico, pero poco realista dado lo económico que salen el coche y la moto.
Lo ha resuelto de una forma muy ortodoxa, utilizando, como el anterior, el método sucesivo. Acomete el primer sustraendo y lo descompone sucesivamente en centenas, decenas y unidades. Una vez que acaba con él, comienza con el segundo sustraendo, al que le aplica la misma técnica.
Esta niña propone un problema lógico, pero menos realista. Emplea el método simultáneo con alguna peculiaridad. Es capaz de reunir en un sólo sustraendo 240 del primero y 314 del segundo, y quita los 554 de una vez.
Pero no tiene seguridad a la hora de cruzar la "frontera" del 300. Por ello, quita 2 y luego 1. Ahora está en condiciones de sustraer números más complicados. Es loque hace juntando los restos de los dos sustraendos y sustrayéndolos de una vez.
No sé lo que son los Monster High, pero el problema es lógico y no puedo juzgar su grado de realismo.
La niña o el niño emplea la técnica simultánea, pero de una forma más canónica que el anterior. Primero quita todas las centenas y luego todas las decenas. Sin embargo, no se atreve a hacer lo mismo con las unidades, y las detrae sucesivamente. ¿Por qué? Pues no lo sabemos, pero les pasa a muchos.
Es lógico y realista, aunque el bosque haya tenido muy mala suerte.
Tiene una técnica buena. En el primer sustraendo recoge todas las centenas, las decenas del primer sustraendo y seis de las unidades del primero, dejando una. Con ello no se complica la vida a la hora de detraer.
Después, no se atreve a descontar veinticinco, sino que primero quita diez para redondear y luego los quince.
El problema es lógico y realista, siempre y cuando que las prendas sean de una marca de bastante lujo.
El método que emplea es el sucesivo, pero ello no es un retroceso. Ni mucho menos. Lo que hace es quitar de una vez cada uno de los sustraendos. Y ninguna de esas sustracciones es fácil.
Es admirable la capacidad de cálculo alcanzada.
Problema lógico y poco realista. Pero es que ha puesto toda su capacidad, que es muchísima, en el cálculo. Es asombroso. Se trata de un niño que está comenzando 3º de Primaria.
Emplea el método simultáneo. Pero casi sobran las palabras. Suma mentalmente 247 y 324 (571) y detrae esa cantidad de golpe, en un único intento.
Para que el lector o lectora se dé cuenta de la dificultad, puede intentar realizar esta operación del mismo modo.
En definitiva, la observación de los trabajos de los niños y niñas nos permite construir el mapa de la evolución del pensamiento matemático de los niños y las fases por las que pasan. Aprendemos mucho, especialmente que los alumnos y alumnas son capaces de hacer cosas mucho más difíciles de las que nos podemos imaginar.
Publicado por
Jaime Martínez Montero
en
17:34
1 comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Doble resta. 3º de Primaria.
domingo, 16 de octubre de 2011
Divisiones sintéticas
No sé si el nombre que le hemos puesto es el más adecuado. El caso es que los niños y niñas resuelven estas divisiones por una cifra prescindiendo de dividendos y restos parciales. Ello supone una gran capacidad de cálculo y una buena memoria de trabajo. No sabemos si esta forma de resolución estará al alcance de todos los niños o solo de unos cuantos. Por ello, se les da la opción de que adopten una u otra forma de resolución según se vean con fuerzas o no para intentarlo por la vía sintética.
La idea nos vino, como en muchas ocasiones, de los niños y de sus maestras. En este caso, la fuente de inspiración fue la resolución de una división entre dos en el CEIP "San José de Clasanza", de Rota, que llevaron a cabo dos niñas (Mireia y Mari Carmen). Los dos vídeos están recogidos en las entradas o posts de finales de Junio de 2011. En ellos se prescindía de los dividendos parciales. Y, claro, si con siete años algunas niñas pueden prescindir del apoyo de escribir los dividendos parciales, ¿no podrían los de nueve años obviar tanto unos como otros? Pues así ha sido.
Los dos niños y la niña lo hacen muy bien. Pero me gustaría hacer notar la enorme seguridad en las respuestas de Fernando. Fíjense bien.
La idea nos vino, como en muchas ocasiones, de los niños y de sus maestras. En este caso, la fuente de inspiración fue la resolución de una división entre dos en el CEIP "San José de Clasanza", de Rota, que llevaron a cabo dos niñas (Mireia y Mari Carmen). Los dos vídeos están recogidos en las entradas o posts de finales de Junio de 2011. En ellos se prescindía de los dividendos parciales. Y, claro, si con siete años algunas niñas pueden prescindir del apoyo de escribir los dividendos parciales, ¿no podrían los de nueve años obviar tanto unos como otros? Pues así ha sido.
Los dos niños y la niña lo hacen muy bien. Pero me gustaría hacer notar la enorme seguridad en las respuestas de Fernando. Fíjense bien.
Publicado por
Jaime Martínez Montero
en
10:21
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
División. 4º de Primaria. Formato sintético.
Sustración en escalera descendente
Los algoritmos ABN son abiertos, pero no sólo para los alumnos. También los maestros introducen variaciones en los formatos. Es el ejemplo de lo ocurrido en este colegio, en el que han optado por este formato para resolver las sustracciones en escalera descendente.
Publicado por
Jaime Martínez Montero
en
10:14
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Sustracción. 4º de Primaria. Formato en escalera descendente.
Sustracción (resta mental)
El alumno iba a realizar una sustracción en escalera, pero dijo que no tenía necesidad de dar pasos intermedios. Y ahí está. La aprovechamos para hacer preguntas que nos mostraran su dominio del algoritmo.
Los niños y niñas del colegio "Lapachar", de Chipiona, comenzaron a trabajar el método ABN el curso pasado, cuando comenzaron Tercero. Hoy, al iniciar Cuarto, son unos expertos.
Los niños y niñas del colegio "Lapachar", de Chipiona, comenzaron a trabajar el método ABN el curso pasado, cuando comenzaron Tercero. Hoy, al iniciar Cuarto, son unos expertos.
Publicado por
Jaime Martínez Montero
en
10:12
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Sustracción. 4º de Primaria. Formato oral.
miércoles, 12 de octubre de 2011
Decoración para la numeración
Números para decorar la clase mientras aprenden la numeración, ilustrados con palillos formando unidades y decenas, coloreando las unidades de azul y las decenas de rojo. Útil sobre todo para introducir los números mediante el algoritmo ABN con apoyo de palillos.
En esta ocasión los 19 primeros números. La hoja correspondiente al 10 se presenta en tres formatos distintos.
Publicado por
José Miguel de la Rosa Sánchez
en
10:45
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Materiales y Generadores.
martes, 11 de octubre de 2011
Manifiesto en contra de los Algoritmos Tradicionales
Ya se pueden imaginar lo de acuerdo que estamos con el contenido del manifiesto. Toda la familia ABN es una propagandista, pero con hechos y con alternativas. Es la línea.
ANÁLISIS Y REFLEXIÓN SOBRE EL MANIFIESTO DEL COLEGIO AGUAMANSA EN CONTRA DE LOS ALGORITMOS TRADICIONALES DE LAS OPERACIONES ARITMÉTICAS
Publicado por
Jaime Martínez Montero
en
17:35
1 comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Artículos.
sábado, 1 de octubre de 2011
Compensar
Esta vez la operación de Compensar la hacen los niños de 2º. Su soltura en el cálculo es admirable, lo que indica el magnífico trabajo que se ha hecho con ellos. Llama la atención cómo sus manos siguen el trabajo de su cerebro. Ha de tenerse en cuenta que, al igual que en el caso de la doble resta, están empezando 2º y nunca habían hecho este tipo de operaciones..
Publicado por
Jaime Martínez Montero
en
0:16
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Reparto igualatorio. 2º de Primaria.
Doble resta
Este niño verifica que la invención de un alumno de su edad, aunque de otro colegio, funciona. Debe ser la conexión generacional. Fíjense en cómo utiliza los dedos para realizar algunos cálculos.
Publicado por
Jaime Martínez Montero
en
0:10
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Doble resta. 2º de Primaria.
Sumiresta.
Las nuevas operaciones han prendido con mucha fuerza. Laura, del CEIP "San Rafael", de Cádiz, la practica con acierto.
Publicado por
Jaime Martínez Montero
en
0:08
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Sumirrestas. 3º de Primaria.
lunes, 26 de septiembre de 2011
El artículo prometido sobre la operación de compensar.
Me han llegado observaciones y sugerencias respecto a la operación de compensar y, específicamente, si la misma no es más que la repetición más o menos disfrazada de las que integran procesos de igualación: resta en escalera ascendente y resta en escalera descendente.
Dada la novedad del planteamiento, no viene mal que hagamos algunas precisiones.
La operación de compensar no implica situaciones de igualación tal y como estas están definidas en la bibliografía al uso. En una situación de igualación, una de las cantidades permanece fija, mientras que es la otra la que experimenta variaciones. En el caso de la compensación, ambas cantidades experimentan cambios y de un tipo muy peculiar: son simultáneos e inversos. Es verdad que se han de igualar las cantidades, pero no se sabe en qué momento se va a producir esta igualación. Es más, averiguarlo es el paso previo para la solución de la operación.
En realidad, la operación de compensar es una suma truncada o interrumpida. Respecto a la suma hay dos diferencias fundamentales. La primera es que en una suma de dos sumandos se va añadiendo uno de ellos al otro, hasta que se agota o desaparece el que se va añadiendo. En el caso de la compensación, el proceso es idéntico, pero sólo hasta que ambos sumandos alcanzan el mismo cardinal. La segunda es que, mientras en la suma el resultado final es el cardinal del sumando al que se ha acumulado el otro, en la operación de compensar el resultado final es la suma de las agregaciones que se han realizado hasta que se ha alcanzado la igualdad entre ambos sumandos.
Pongamos un ejemplo para aclarar lo explicado. Sea la suma 68+42. En esencia, se irán acumulando los 42 elementos del segundo sumando en el primero. Se hará hasta que se agote el sumando 42, y el resultado será lo que resulte de tal acumulación (110). En el caso de la operación de compensar, se hace trasvase siempre desde el mayor al menor, y sólo hasta que se igualan ambos sumandos. En este caso, cuando se traspasan 13, ambos sumandos quedan en 55. El resultado no es la acumulación de uno de los sumandos, sino la parte que se ha traspasado (13).
Respecto al tipo de problemas que venga a resolver, los de compensación son de dos o tres operaciones, y encajan en la categoría semántica de “Compartir el todo”, según la terminología de Nesher y Herskovitz. Normalmente hay dos vías alternativas para su resolución. La más general es la suma de las cantidades iniciales y la posterior división por dos para hallar el punto de igualdad. A partir de ahí, se detrae esa cantidad del sumando mayor para averiguar el cardinal del traspaso. En el ejemplo que venimos usando sería: 68+42= 110; 110: 2= 55; 68-55=13. La segunda es más rápida, más difícil de conceptualizar y tiene más complicada aplicación cuando se trate de compensar en el caso de que hubiera tres sujetos o más. En el mismo ejemplo: primero se establece la diferencia (68-42=26) y luego esa diferencia se divide entre dos (26:2=13). Se obtiene así directamente el resultado. En cualquier caso es un problema difícil. Nótese que es de los pocos que ofrece sólo dos datos y, sin embargo, puede comprender hasta tres operaciones.
¿Cuál es nuestro propósito al introducir esta nueva operación? No, desde luego, que resuelvan los alumnos las compensaciones por ensayo y error. Pero sí que, antes de abordar la solución aritmética, entiendan conceptualmente qué significa la compensación, qué características tiene y cómo pueden desarrollar una capacidad estimativa que les ahorre los cálculos cuando la precisión que se les exija lo permita.
Publicado por
Jaime Martínez Montero
en
18:23
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Reparto Igualatorio.
Preguntas fáciles y difíciles sobre la multiplicación.
X 7 | ||
6000 | 42.000 | |
800 | 5600 | 47.600 |
30 | 210 | 47.810 |
4 | 28 | 47.838 |
¿Cuántos se necesitarían si sólo se repartiera 6000? ( y así todos los multiplicandos parciales).
¿Cuántas se necesitarían si sólo se repartieran 6800? (47.600)
¿Cuántas se necesitarían si se repartieran 6830? (47.810)
PREGUNTAS DIFÍCILES.
¿Cuántas se necesitarían si se repartiera 6030? (42.210)
¿Y si fueran 6004? (42.028)
¿Y si fueran 830? (5810)
¿Y si fueran 834? (5828)
PREGUNTAS MUY DIFÍCILES.
¿Cuántas se necesitarían si en lugar de repartir a 7 se repartieran sólo a 6? (41.004)
¿Cuántas se necesitarían si en lugar de repartir a 7 se repartieran a 8? (54.672)
Publicado por
Jaime Martínez Montero
en
18:21
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Producto.
Suscribirse a:
Entradas (Atom)