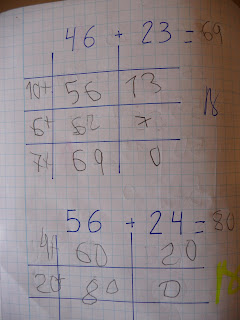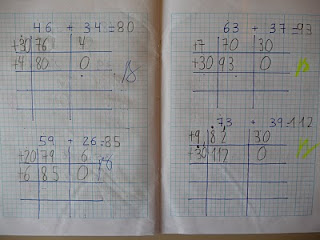En el siguiente enlace se puede ver el reportaje que Canal Sur Andalucía emitió en sus espacios de noticias de medidodía y tarde-noche el día 24 de Marzo.
http://www.radiotelevisionandalucia.es/tvcarta/impe/web/contenido?id=5232
Páginas
▼
lunes, 29 de marzo de 2010
viernes, 26 de marzo de 2010
¡Más difícil todavía! Los alumnos de 2º del CEIP "Andalucía", de Cádiz, hacen sumas de tres sumandos ... con decimales.
Primer ejemplo. Ellos, naturalmente, no hablan de décimas ni centésimas, sino de euros y céntimos de euros. Este alumno ha seguido un camino muy prudente. Ha agotado en primer lugar el sumando final, y tras ello ha sumado los cuatro céntimos.
Ha realizado la operación en los mismos cuatro intentos con los que hubiera tenido que realizarla de haberse presentado la misma en el formato tradicional. En este caso, desaparece el problema de la "colocación" de los sumandos.
Ahora es una niña la que hace la operación. Es algo más rápida, pues el sumando final lo acumula en dos veces, en lugar de en tres, como en el caso anterior.
Como los del Señor, los caminos de los niños (de esta niña en concreto) son inescrutables. Pasa con mucha precaución las décimas del tercer sumando al segundo sumando, luego las centésimas. Y, lo más difícil: suma de una vez 0,77 con 10,82. Pues si sabe hacer este cálculo, ¿para qué tomó tantas precauciones?
Este niño calcula muy bien. ¿Que hay que acumular un sumando? Lo arregla con un intento. ¿Que hay que hacerlo con dos sumandos? Pues con dos. Así de sencillo. Ahora bien, si su maestra no le insiste en que de vez en cuando debe reflejar los cálculos por escrito, hace todo mentalmente.
El cálculo ABN pone bien de manifiesto que no hay dos casos iguales. Comparen la operación de esta niña con la anterior.
¿Y este niño? También es de los que no necesita hacer el cálculo escrito. Y establece sus propios códigos. Así, en los residuos de los sumandos segundo y tercero escribe los céntimos como si fueran enteros. Pero no obra así cuando expresa la cantidad que va a sumar o la acumulación parcial o total.
Una última muestra de otro alumnos. ¿Sabe o no sabe lo que se trae entre manos?
Ha realizado la operación en los mismos cuatro intentos con los que hubiera tenido que realizarla de haberse presentado la misma en el formato tradicional. En este caso, desaparece el problema de la "colocación" de los sumandos.
Ahora es una niña la que hace la operación. Es algo más rápida, pues el sumando final lo acumula en dos veces, en lugar de en tres, como en el caso anterior.
Como los del Señor, los caminos de los niños (de esta niña en concreto) son inescrutables. Pasa con mucha precaución las décimas del tercer sumando al segundo sumando, luego las centésimas. Y, lo más difícil: suma de una vez 0,77 con 10,82. Pues si sabe hacer este cálculo, ¿para qué tomó tantas precauciones?
Este niño calcula muy bien. ¿Que hay que acumular un sumando? Lo arregla con un intento. ¿Que hay que hacerlo con dos sumandos? Pues con dos. Así de sencillo. Ahora bien, si su maestra no le insiste en que de vez en cuando debe reflejar los cálculos por escrito, hace todo mentalmente.
El cálculo ABN pone bien de manifiesto que no hay dos casos iguales. Comparen la operación de esta niña con la anterior.
¿Y este niño? También es de los que no necesita hacer el cálculo escrito. Y establece sus propios códigos. Así, en los residuos de los sumandos segundo y tercero escribe los céntimos como si fueran enteros. Pero no obra así cuando expresa la cantidad que va a sumar o la acumulación parcial o total.
Una última muestra de otro alumnos. ¿Sabe o no sabe lo que se trae entre manos?
jueves, 18 de marzo de 2010
Los alumnos de 2º de Primaria del CEIP "Andalucía", de Cádiz, ya hacen operaciones de sumar con tres sumandos.
Los alumnos de 2º de Primaria siguen unas pautas bastante interesantes cuando resuelven las operaciones
 ABN de sumar con tres términos. En el ejemplo de la fotografía, el alumno ha "agotado" en primer lugar el sumando 137, y una vez que ha terminado con él, inicia la acumulación del 51. Sigue así un modelo sucesivo de agrupación. Es el más común, y en el que en este momento está un tercio de los alumnos.
ABN de sumar con tres términos. En el ejemplo de la fotografía, el alumno ha "agotado" en primer lugar el sumando 137, y una vez que ha terminado con él, inicia la acumulación del 51. Sigue así un modelo sucesivo de agrupación. Es el más común, y en el que en este momento está un tercio de los alumnos.El modelo sucesivo no está exento de complicación. Por ejemplo, en el presente caso el sujeto se complica el cálculo porque opta por acumular los dos sumandos mayores en el menor.

Un paso adelante en el dominio de los cálculos supone la utilización simultánea de los dos sumandos para hallar la suma total. En el caso de la fotografía, el alumno lleva a cabo una técnica de apoyo muy interesante: escribe a la izquierda lo que detrae de cada uno de los sumandos.
Se sigue mejorando. Ahora ya se expresa en un solo número (situado a la izquierda del resultado de los cálculos) lo que va a acumular en el sumando mayor. En la segunda línea del ejemplo añade 60, que forma extrayendo 30 de lo que quedaba del último sumando (137) y otros 30 del segundo sumando (51).
Último ejemplo: un sujeto muy competente. Realiza el cálculo en solo dos pasos, que es uno menos de los que tendría que utilizar en el caso de la vieja cuenta de sumar.
Primero ha cogido 100 y 50, y finalmente ha sumado los 38 restantes de una vez.
¿Y ESTE? ¿CÓMO LO HACE?
Como bien dice una maestra de estos niños, cada uno hace la operación como le sale del alma. Eso es verdad y eso es bueno. Aquí tienen un ejemplo. ¿Cómo la ha hecho? Porque la ha hecho bien y no se ha copiado de nadie.
sábado, 13 de marzo de 2010
¿CUÁNTAS OPERACIONES DE RESTAR HAY?
El algoritmo de la resta es el modelo formal que resuelve muchas y diferentes situaciones problemáticas. De acuerdo con la tipificación de las mismas que hacen los expertos, hasta trece problemas diferentes de restar son susceptibles de ser propuestos en la educación primaria. No es que sólo haya trece problemas que se solucionen a través de una sustracción, sino que toda la variedad e infinidad de problemas de este tipo se pueden reducir o encajan dentro de los trece que recogen los modelos más comúnmente admitidos por los expertos.
Ahora bien, que los alumnos de los primeros cursos de Educación Primaria sean capaces de pasar desde los trece tipos diferentes, con sus significados a veces contrapuestos, a un único modelo formal de algoritmo, es algo que no es posible para la gran mayoría de los alumnos. Si, además, el formato que se emplea es el tradicional (que carece por completo de sentido para los niños), la tarea se reduce a un ejercicio de adivinación o de suerte.
Por ello, creemos que debe existir una situación intermedia, unos formatos mediadores entre las trece situaciones típicas y la llegada a un único modelo de algoritmo. Las trece situaciones se pueden subsumir en cuatro acciones fundamentales:
SUSTRAER O QUITAR: Se tiene una cantidad, y de ella se pierde, se quita o se regala, y se averigua lo que falta.
COMPARAR: Se tienen dos cantidades, y se desea saber en cuánto se diferencia la una de la otra.
AÑADIR HASTA: Se tiene una cantidad, a la que hay que añadir otra hasta llegar a la que se marcado como meta.
DESCENDER HASTA: Es la inversa a la anterior. Desde una determinada cantidad se quiere llegar a otra más pequeña, y hay que averiguar cuánto tenemos que quitar.
Pongamos algunos ejemplos.
1. Se tienen 8506 € y se gastan 3497. ¿Cuánto queda? La primera columna es lo que se tiene, la segunda lo que se gasta, y la tercera las cantidades parciales que se van detrayendo.
2. Un pueblo tiene 8506 habitantes y otro 3497. ¿Cuántos vecinas más tiene el primero? Quedan claras las dos primeras columnas. La tercera son los vecinos que se van quitando a la vez hasta que se llegue a cero en la cantidad menor. Lo que quede de la mayor es la diferencia.
Los tipos de problema que admite este formato son:
“Tengo 83 € y me gasto 46. ¿Cuánto dinero me queda?” (CA2).
“En el colegio hay 452 estudiantes. 243 son chicos y las restantes son chicas. ¿Cuántas chicas hay?” (CO2).
“Tengo 94 cromos. Tú tienes 34 cromos menos que yo. ¿Cuántos tienes tú?” (CM4).
“Tengo 48 €, y tengo 24 € más que tú. ¿Cuántos tienes tú?” (CM5).
“En el colegio somos 253 estudiantes. Si en el colegio de enfrente hubiera 67 estudiantes más habría los mismos que en mi colegio. ¿Cuántos chicos y chicas tiene el otro colegio?” (IG3).
“Tengo 94 cromos. Si perdiera 34 tendría los mismos que Raquel. ¿Cuántos cromos tiene Raquel?” (IG6).
“Mi abuelo tiene 67 años, y mi madre 34. ¿Cuántos años más tiene mi abuelo?” (CM1) o “¿cuántos años menos tiene mi madre?” (CM2).
AÑADIR HASTA. Es el formato en escalera ascendente. Sólo requiere de dos columnas. En una se refleja la cantidad que se va a subir, y en la otra el punto en el que se ha llegado.
En el modelo de escalera ascendente encajan tres tipos de problemas:
“Mi padre ha ido al banco con 152 €. Ha sacado dinero y ahora tiene 232. ¿Cuánto dinero ha sacado?” (CA3).
“Mi madre me ha regalado 62 cromos. Con esos y con los que tenía reúno 89. ¿Cuántos tenía antes del regalo de mi madre?” (CA5).
"Una PSP cuesta 345 €. Yo tengo 126. ¿Cuánto dinero me tienen que dar para que pueda comprarla?” (IG1).
DESCENDER HASTA. También requiere de dos columnas. En la primera va la cantidad a bajar, y en la segunda el punto al que se ha llegado. La foto ilustra lo que se quiere señalar.
Dos tipos de problemas se adecuan a este formato:
“He ido a jugar con 32 canicas. He perdido, y ahora me quedan 17. ¿Cuántas he perdido?” (CA4).
“Mi amiga Ana tiene 68 € en su hucha, y yo tengo 37. ¿Cuántos tiene que sacar Ana para que en su hucha le quede el mismo dinero que a mí?” (IG2).
Ahora bien, que los alumnos de los primeros cursos de Educación Primaria sean capaces de pasar desde los trece tipos diferentes, con sus significados a veces contrapuestos, a un único modelo formal de algoritmo, es algo que no es posible para la gran mayoría de los alumnos. Si, además, el formato que se emplea es el tradicional (que carece por completo de sentido para los niños), la tarea se reduce a un ejercicio de adivinación o de suerte.
Por ello, creemos que debe existir una situación intermedia, unos formatos mediadores entre las trece situaciones típicas y la llegada a un único modelo de algoritmo. Las trece situaciones se pueden subsumir en cuatro acciones fundamentales:
SUSTRAER O QUITAR: Se tiene una cantidad, y de ella se pierde, se quita o se regala, y se averigua lo que falta.
COMPARAR: Se tienen dos cantidades, y se desea saber en cuánto se diferencia la una de la otra.
AÑADIR HASTA: Se tiene una cantidad, a la que hay que añadir otra hasta llegar a la que se marcado como meta.
DESCENDER HASTA: Es la inversa a la anterior. Desde una determinada cantidad se quiere llegar a otra más pequeña, y hay que averiguar cuánto tenemos que quitar.
Pongamos algunos ejemplos.
SUSTRAER y COMPARAR pueden ser subsumidas en un mismo formato. Éste consta de tres columnas: las dos que corresponden a las cantidades y lo que se quita de las dos (en la comparación) y en la detracción, la que corresponde a la cantidad que se tiene, lo que hay que quitar y las sucesivas quitas que se van realizando. En el ejemplo ilustrado por la foto se pueden seguir los dos problemas:
1. Se tienen 8506 € y se gastan 3497. ¿Cuánto queda? La primera columna es lo que se tiene, la segunda lo que se gasta, y la tercera las cantidades parciales que se van detrayendo.
2. Un pueblo tiene 8506 habitantes y otro 3497. ¿Cuántos vecinas más tiene el primero? Quedan claras las dos primeras columnas. La tercera son los vecinos que se van quitando a la vez hasta que se llegue a cero en la cantidad menor. Lo que quede de la mayor es la diferencia.
Los tipos de problema que admite este formato son:
“Tengo 83 € y me gasto 46. ¿Cuánto dinero me queda?” (CA2).
“En el colegio hay 452 estudiantes. 243 son chicos y las restantes son chicas. ¿Cuántas chicas hay?” (CO2).
“Tengo 94 cromos. Tú tienes 34 cromos menos que yo. ¿Cuántos tienes tú?” (CM4).
“Tengo 48 €, y tengo 24 € más que tú. ¿Cuántos tienes tú?” (CM5).
“En el colegio somos 253 estudiantes. Si en el colegio de enfrente hubiera 67 estudiantes más habría los mismos que en mi colegio. ¿Cuántos chicos y chicas tiene el otro colegio?” (IG3).
“Tengo 94 cromos. Si perdiera 34 tendría los mismos que Raquel. ¿Cuántos cromos tiene Raquel?” (IG6).
“Mi abuelo tiene 67 años, y mi madre 34. ¿Cuántos años más tiene mi abuelo?” (CM1) o “¿cuántos años menos tiene mi madre?” (CM2).
AÑADIR HASTA. Es el formato en escalera ascendente. Sólo requiere de dos columnas. En una se refleja la cantidad que se va a subir, y en la otra el punto en el que se ha llegado.
En el modelo de escalera ascendente encajan tres tipos de problemas:
“Mi padre ha ido al banco con 152 €. Ha sacado dinero y ahora tiene 232. ¿Cuánto dinero ha sacado?” (CA3).
“Mi madre me ha regalado 62 cromos. Con esos y con los que tenía reúno 89. ¿Cuántos tenía antes del regalo de mi madre?” (CA5).
"Una PSP cuesta 345 €. Yo tengo 126. ¿Cuánto dinero me tienen que dar para que pueda comprarla?” (IG1).
DESCENDER HASTA. También requiere de dos columnas. En la primera va la cantidad a bajar, y en la segunda el punto al que se ha llegado. La foto ilustra lo que se quiere señalar.
Dos tipos de problemas se adecuan a este formato:
“He ido a jugar con 32 canicas. He perdido, y ahora me quedan 17. ¿Cuántas he perdido?” (CA4).
“Mi amiga Ana tiene 68 € en su hucha, y yo tengo 37. ¿Cuántos tiene que sacar Ana para que en su hucha le quede el mismo dinero que a mí?” (IG2).
lunes, 8 de marzo de 2010
ASÍ EMPEZARON LAS PRIMERAS SUMAS. PRIMERO DE PRIMARIA.
SAMARA. En la primera operación toma la vía más expeditiva: añade primero las unidades y luego las decenas. Sin embargo no hace igual en la segunda operación, porque se toma bastantes precauciones para resolverla. Pasa cinco de veinticinco a treinta y nueve, y vuelve a dejar el 20. Pero en lugar de hacer lo que en la operación anterior, opta por descomponerlo e ir añadiendo poco a poco: cuatro, después seis y, en lugar de pasar las diez restantes de golpe, los subdivide en dos de cinco.
La virtualidad del sistema es precisamente que cada alumno puede hacer las operaciones de la forma que considere oportuna y de la manera que le dé más seguridad.
ANA. En las tres operaciones se revelan tres estilos distintos: rapidez en 27+22; prudencia y parsimonia en 34+16; finalmente, sistematicidad en 42+34.
En el tránsito de la primera a la tercera operación se da un proceso de autoaprendizaje, que se puede ver en más casos que no podemos traer aquí.
LIDIA. La operación 43 +29 es muy importante. En primer lugar añade dos, y luego siete, con el fin de redondear. Dejándose llevar de una estrategia, dice que va a agregar diez. Pero se da cuenta de que puede sumar los veinte de una vez. Y así lo hace, olvidándose del diez que había escrito en la primera fila de la izquierda. Es otra muestra del alto poder de autoaprendizaje que tiene el algoritmo ABN.
En el caso de 37 + 32 el procedimiento es el mismo: redondea y suma diez. Lo que ocurre es que aquí no tuvo la “ocurrencia” de la operación anterior. Cuando ha de sumar 49 y 20, descompone éste sucesivamente en dos dieces. ¿Tal vez porque en la cuenta anterior era añadir a una cifra de unidades baja, y aquí se trata de hacerlo con una alta?
SALVI. Es un alumno con dificultades, pero al que se le dan bien las matemáticas.
En las dos operaciones presenta estrategias distintas. En el caso de 46 + 23 lleva a cabo un cálculo curioso: cuando queda con trece no añade primero diez y luego tres, sino que descompone el trece en seis y siete.
En 56 + 24 emplea dos pasos: decenas y unidades. Utiliza la estrategia más clásica. Choca, sin embargo, que varíe tanto el cálculo del sumando 23 de la primera operación, al sumando 24 de la segunda. Tal vez el sentido de inventar o descubrir que el algoritmo ofrece al alumno sea la causa que explique estos diversos comportamientos.
ÓSCAR. Esta alumno ha vencido algunas de las dificultades que presentaron los anteriores.
La operación más interesante es 82+59. Parece que la hace poniéndose a prueba, constatando que puede hacer lo que hace. Cuando se queda con cincuenta y puede pasar de diez en diez, pasa cinco, y cuando se queda con 45 es cuando pasa diez. “Remata” la faena añadiendo treinta de golpe.
FRANCISCO JOSÉ. Es a la vez ortodoxia y prudencia. Lo primero que hace es dejar sin unidades al sumando que va a añadir, y luego va acabando con él traspasándolo al mayor de diez en diez.
MARIO. Se trata de un niño despabilado, que aplica una sistemática que le permite resolver cualquier operación en dos pasos. Bien es verdad que no sigue siempre el orden unidad-decena, pero tal asunto aparece irrelevante.
ALICIA. Es una alumna bien dotada para el cálculo. Redondea en el sumando más pequeño y añade de una vez las decenas. En la realidad, casi siempre hace el cálculo directamente, sin necesidad de los pasos intermedios.
ALICIA 2. Hemos traído a esta niña para mostrar cómo resta. Se refleja en la siguiente fotografía. De las cuatro formas distintas de sustraer, se ha iniciado en la que consiste en detraer el mismo número de los dos miembros, hasta que hace desaparecer uno y lo que queda del otro es el resultado. Nótese la soltura que tiene cuando extrae quince de ciento dos. ¿Cómo lo hace? Quita mentalmente una decena (llega a noventa y dos) y tras ello sustrae cinco.
No es tan difícil sustraer para los aniños y niñas que practican esta técnica. Cualquier suma, de hecho, implica siempre sustracciones.
La prensa da la noticia de los buenos resultados del método.
En el enlace siguiente se puede leer la noticia de los buenos resultados obtenidos por nuestro método en una evaluación intermedia de control.
http://www.diariodecadiz.es/article/provincia/647890/experimento/calculo/primaria/supera/la/evaluacion.html
Espero que la lean, la valoren y la comenten.
http://www.diariodecadiz.es/article/provincia/647890/experimento/calculo/primaria/supera/la/evaluacion.html
Espero que la lean, la valoren y la comenten.
domingo, 7 de marzo de 2010
¿Qué ventajas ofrecen los algoritmos ABN frente a las cuentas de toda la vida?
Muchas. Pero se han de señalar:
MÁS FLEXIBILIDAD. Al no haber una única forma de resolverlo, cada niño o niña puede hacerlo según sus propias características. Un alumno rápido llegará muy deprisa a la solución. Otro más lento dará más rodeos. El que sea muy meticuloso alargará el algoritmo, mientras que el intuitivo descubrirá formas nuevas de acortarlo. En la foto que ofrecemos se ve cómo la misma operación es resuelta de manera muy diferente por los alumnos.
FACILITA LA RESOLUCIÓN DE PROBLEMAS. El proceso de realización del algoritmo es transparente, pleno de sentido, y controlado paso a paso por el alumno. Por ello, la resolución de problemas mejora de manera inmediata. Es más, al ser un algoritmo con sentido, el niño rectifica los errores tan pronto se da cuenta de que ha elegido mal el modelo. El trabajar con números completos, y no con cifras, ayuda mucho a que se sepa lo que se hace.
ELIMINA LA MAYOR PARTE DE LAS DIFICULTADES DEL CÁLCULO. Así es. Con estos algoritmos se acaba el problema de las llevadas, tanto en la suma como en la resta. También desaparece el problema de la colocación, el orden de los términos, etc. En la mutliplicación no plantean dificultades los ceros intercalados, ni hay nada parecido al orden o colocación. En la división desaparece el problema del cero al cociente intermedio o final. Todo lo que decimos es de aplicación también a las operaciones con decimales, que tienen un tratamiento tan natural que permiten que los niños de 2º de Primaria puedan, desde el segundo trimestre, sumar y restar con números que incluyen décimas y centésimas.
PERMITE APROVECHAR LA EXPERIENCIA DEL PROPIO ALUMNO. Es que es la experiencia del propio alumno la que guía la resolución del algoritmo. El formato del mismo facilita que se integre su forma de trabajar y su saber en la tarea escolar diaria.
FOMENTA LA ESTIMACIÓN Y EL CÁLCULO MENTAL. Es este tal vez el rasgo que más espectacularidad da al proceso de resolución. Algún maestro ha comentado, viendo resolver cálculos a los niños de 2º, que eso no son capaces de hacerlo los chicos y chicas de 6º. Y es verdad. Con un buen entrenamiento y una adecuada secuenciación, los alumnos alcanzan una enorme destreza.
MÁS FLEXIBILIDAD. Al no haber una única forma de resolverlo, cada niño o niña puede hacerlo según sus propias características. Un alumno rápido llegará muy deprisa a la solución. Otro más lento dará más rodeos. El que sea muy meticuloso alargará el algoritmo, mientras que el intuitivo descubrirá formas nuevas de acortarlo. En la foto que ofrecemos se ve cómo la misma operación es resuelta de manera muy diferente por los alumnos.
FACILITA LA RESOLUCIÓN DE PROBLEMAS. El proceso de realización del algoritmo es transparente, pleno de sentido, y controlado paso a paso por el alumno. Por ello, la resolución de problemas mejora de manera inmediata. Es más, al ser un algoritmo con sentido, el niño rectifica los errores tan pronto se da cuenta de que ha elegido mal el modelo. El trabajar con números completos, y no con cifras, ayuda mucho a que se sepa lo que se hace.
ELIMINA LA MAYOR PARTE DE LAS DIFICULTADES DEL CÁLCULO. Así es. Con estos algoritmos se acaba el problema de las llevadas, tanto en la suma como en la resta. También desaparece el problema de la colocación, el orden de los términos, etc. En la mutliplicación no plantean dificultades los ceros intercalados, ni hay nada parecido al orden o colocación. En la división desaparece el problema del cero al cociente intermedio o final. Todo lo que decimos es de aplicación también a las operaciones con decimales, que tienen un tratamiento tan natural que permiten que los niños de 2º de Primaria puedan, desde el segundo trimestre, sumar y restar con números que incluyen décimas y centésimas.
PERMITE APROVECHAR LA EXPERIENCIA DEL PROPIO ALUMNO. Es que es la experiencia del propio alumno la que guía la resolución del algoritmo. El formato del mismo facilita que se integre su forma de trabajar y su saber en la tarea escolar diaria.
FOMENTA LA ESTIMACIÓN Y EL CÁLCULO MENTAL. Es este tal vez el rasgo que más espectacularidad da al proceso de resolución. Algún maestro ha comentado, viendo resolver cálculos a los niños de 2º, que eso no son capaces de hacerlo los chicos y chicas de 6º. Y es verdad. Con un buen entrenamiento y una adecuada secuenciación, los alumnos alcanzan una enorme destreza.
¡No somos los únicos!
El Colegio Público "Aguamansa", de La Orotava, ha roto también con las viejas cuentas. Los chicos y chicas de este colegio calculan con una originalidad y rapidez tal que da gusto verlos. ¿Desea comprobarlo? Pruebe con este enlace:
http://www.aguamansa.es/aguamansa.html
http://www.aguamansa.es/aguamansa.html
¿Dónde se lleva a cabo la experiencia?
En el presente curso (2009-2010) la experiencia de renovar por completo la enseñanza del cálculo a través de la metodología basada en los algoritmos ABN se está llevando a cabo en los siguientes colegios y cursos:
CÁDIZ: Colegio Público "Andalucía". Cursos 1º y 2º de Primaria. Dos grupos de alumnos.
Colegio Público "Carlos III". Curso 2º de Primaria. Un grupo de alumnos.
PUERTO REAL: Colegio Público "Reggio". Cursos 1º y 4º de Primaria. Dos grupos de alumnos.
Colegio Público "Reyes Católicos". Cursos 2º y 5º de Primaria. Tres grupos de alumnos.
Mi agradecimiento a las Maestras (y al maestro) que llevan adelante esta profunda innovación, y al apoyo recibido por la dirección de los centros y las familias de los niños.
CÁDIZ: Colegio Público "Andalucía". Cursos 1º y 2º de Primaria. Dos grupos de alumnos.
Colegio Público "Carlos III". Curso 2º de Primaria. Un grupo de alumnos.
PUERTO REAL: Colegio Público "Reggio". Cursos 1º y 4º de Primaria. Dos grupos de alumnos.
Colegio Público "Reyes Católicos". Cursos 2º y 5º de Primaria. Tres grupos de alumnos.
Mi agradecimiento a las Maestras (y al maestro) que llevan adelante esta profunda innovación, y al apoyo recibido por la dirección de los centros y las familias de los niños.
NUESTRA EXPERIENCIA ENCUENTRA ECO.
viernes, 5 de marzo de 2010
LAS CINCO RAZONES POR LAS QUE SE DEBERÍAN PROSCRIBIR LAS VIEJAS CUENTAS.
1. Porque haciendo cuentas no se calcula. Se hace otra cosa. En concreto: se memorizan bases de datos (las tablas) y un conjunto de instrucciones sobre el manejo y la aplicación de las mismas. Nada más. No hay cálculo. Lo que el alumno hace es recuperar de la memoria las combinaciones de las bases de datos y las instrucciones de uso.
2. Porque entorpecen el cálculo mental y la estimación. Nuestro cerebro calcula espontáneamente de izquierda a derecha, y las viejas cuentas (salvo la división), lo hacen en sentido contrario. Son un obstáculo y sólo por esta razón ya se deberían eliminar.
3. Porque ya nadie las hace. Han quedado obsoletas. El lector o lectora que tenga la paciencia de leer esto puede preguntarse: ¿cuándo fue la última vez que hizo una cuenta de dividir por dos cifras? Posiblemente, desde la escuela no haya repetido. ¿De verdad cree alguien que un niño de diez años, por ejemplo, va a hacer cuentas cuando tenga 30 ó 40?
4. Porque son las culpables de que los alumnos no sepan resolver problemas. Se le echa la culpa de tan acreditada incapacidad a la escasa comprensión lectora de chicos y chicas. Pero resulta que sí entienden largos textos y con un vocabulario más elaborado y menos tópico que el que aparece en un problema. No, no es esta la causa. La causa radica en las cuentas. Lo que el alumno hace al realizar cuentas no tiene nada que ver con resolver problemas. ¿Qué se hace cuando se resuelve una cuenta? Veamos. El niño coge dos números, los desmenuza en cada una de sus cifras, y a continuación va emparejando esas cifras desencajadas una a una. Busca en su memoria el resultado del emparejamiento y, conforme a las instrucciones de uso aprendidas previamente, coloca el resultado en su lugar. ¿De dónde va a sacar el alumno la suficiente significación para convertir un proceso ciego, sin sentido, en otro que sí lo tiene? Por eso, el alumno se agarra a un clavo ardiendo cuando se trata de resolver un problema. Y cuando el texto le da la más mínima pista, a ella se acoge. Si aparece “más” sumará (aunque hubiera que restar) y si aparece “entre” dividirá (aunque haya que multiplicar).
5. Porque tienen buena parte de culpa en que los alumnos le tengan tanta tirria a la materia. Se convierten en una tarea tediosa, sin sentido, repetitiva, en la que no interviene la inteligencia. Parece que su finalidad fuera más la de domar a los niños que la de desarrollar su intelecto.
2. Porque entorpecen el cálculo mental y la estimación. Nuestro cerebro calcula espontáneamente de izquierda a derecha, y las viejas cuentas (salvo la división), lo hacen en sentido contrario. Son un obstáculo y sólo por esta razón ya se deberían eliminar.
3. Porque ya nadie las hace. Han quedado obsoletas. El lector o lectora que tenga la paciencia de leer esto puede preguntarse: ¿cuándo fue la última vez que hizo una cuenta de dividir por dos cifras? Posiblemente, desde la escuela no haya repetido. ¿De verdad cree alguien que un niño de diez años, por ejemplo, va a hacer cuentas cuando tenga 30 ó 40?
4. Porque son las culpables de que los alumnos no sepan resolver problemas. Se le echa la culpa de tan acreditada incapacidad a la escasa comprensión lectora de chicos y chicas. Pero resulta que sí entienden largos textos y con un vocabulario más elaborado y menos tópico que el que aparece en un problema. No, no es esta la causa. La causa radica en las cuentas. Lo que el alumno hace al realizar cuentas no tiene nada que ver con resolver problemas. ¿Qué se hace cuando se resuelve una cuenta? Veamos. El niño coge dos números, los desmenuza en cada una de sus cifras, y a continuación va emparejando esas cifras desencajadas una a una. Busca en su memoria el resultado del emparejamiento y, conforme a las instrucciones de uso aprendidas previamente, coloca el resultado en su lugar. ¿De dónde va a sacar el alumno la suficiente significación para convertir un proceso ciego, sin sentido, en otro que sí lo tiene? Por eso, el alumno se agarra a un clavo ardiendo cuando se trata de resolver un problema. Y cuando el texto le da la más mínima pista, a ella se acoge. Si aparece “más” sumará (aunque hubiera que restar) y si aparece “entre” dividirá (aunque haya que multiplicar).
5. Porque tienen buena parte de culpa en que los alumnos le tengan tanta tirria a la materia. Se convierten en una tarea tediosa, sin sentido, repetitiva, en la que no interviene la inteligencia. Parece que su finalidad fuera más la de domar a los niños que la de desarrollar su intelecto.