Páginas
▼
lunes, 8 de marzo de 2010
ASÍ EMPEZARON LAS PRIMERAS SUMAS. PRIMERO DE PRIMARIA.
SAMARA. En la primera operación toma la vía más expeditiva: añade primero las unidades y luego las decenas. Sin embargo no hace igual en la segunda operación, porque se toma bastantes precauciones para resolverla. Pasa cinco de veinticinco a treinta y nueve, y vuelve a dejar el 20. Pero en lugar de hacer lo que en la operación anterior, opta por descomponerlo e ir añadiendo poco a poco: cuatro, después seis y, en lugar de pasar las diez restantes de golpe, los subdivide en dos de cinco.
La virtualidad del sistema es precisamente que cada alumno puede hacer las operaciones de la forma que considere oportuna y de la manera que le dé más seguridad.
ANA. En las tres operaciones se revelan tres estilos distintos: rapidez en 27+22; prudencia y parsimonia en 34+16; finalmente, sistematicidad en 42+34.
En el tránsito de la primera a la tercera operación se da un proceso de autoaprendizaje, que se puede ver en más casos que no podemos traer aquí.
LIDIA. La operación 43 +29 es muy importante. En primer lugar añade dos, y luego siete, con el fin de redondear. Dejándose llevar de una estrategia, dice que va a agregar diez. Pero se da cuenta de que puede sumar los veinte de una vez. Y así lo hace, olvidándose del diez que había escrito en la primera fila de la izquierda. Es otra muestra del alto poder de autoaprendizaje que tiene el algoritmo ABN.
En el caso de 37 + 32 el procedimiento es el mismo: redondea y suma diez. Lo que ocurre es que aquí no tuvo la “ocurrencia” de la operación anterior. Cuando ha de sumar 49 y 20, descompone éste sucesivamente en dos dieces. ¿Tal vez porque en la cuenta anterior era añadir a una cifra de unidades baja, y aquí se trata de hacerlo con una alta?
SALVI. Es un alumno con dificultades, pero al que se le dan bien las matemáticas.
En las dos operaciones presenta estrategias distintas. En el caso de 46 + 23 lleva a cabo un cálculo curioso: cuando queda con trece no añade primero diez y luego tres, sino que descompone el trece en seis y siete.
En 56 + 24 emplea dos pasos: decenas y unidades. Utiliza la estrategia más clásica. Choca, sin embargo, que varíe tanto el cálculo del sumando 23 de la primera operación, al sumando 24 de la segunda. Tal vez el sentido de inventar o descubrir que el algoritmo ofrece al alumno sea la causa que explique estos diversos comportamientos.
ÓSCAR. Esta alumno ha vencido algunas de las dificultades que presentaron los anteriores.
La operación más interesante es 82+59. Parece que la hace poniéndose a prueba, constatando que puede hacer lo que hace. Cuando se queda con cincuenta y puede pasar de diez en diez, pasa cinco, y cuando se queda con 45 es cuando pasa diez. “Remata” la faena añadiendo treinta de golpe.
FRANCISCO JOSÉ. Es a la vez ortodoxia y prudencia. Lo primero que hace es dejar sin unidades al sumando que va a añadir, y luego va acabando con él traspasándolo al mayor de diez en diez.
MARIO. Se trata de un niño despabilado, que aplica una sistemática que le permite resolver cualquier operación en dos pasos. Bien es verdad que no sigue siempre el orden unidad-decena, pero tal asunto aparece irrelevante.
ALICIA. Es una alumna bien dotada para el cálculo. Redondea en el sumando más pequeño y añade de una vez las decenas. En la realidad, casi siempre hace el cálculo directamente, sin necesidad de los pasos intermedios.
ALICIA 2. Hemos traído a esta niña para mostrar cómo resta. Se refleja en la siguiente fotografía. De las cuatro formas distintas de sustraer, se ha iniciado en la que consiste en detraer el mismo número de los dos miembros, hasta que hace desaparecer uno y lo que queda del otro es el resultado. Nótese la soltura que tiene cuando extrae quince de ciento dos. ¿Cómo lo hace? Quita mentalmente una decena (llega a noventa y dos) y tras ello sustrae cinco.
No es tan difícil sustraer para los aniños y niñas que practican esta técnica. Cualquier suma, de hecho, implica siempre sustracciones.



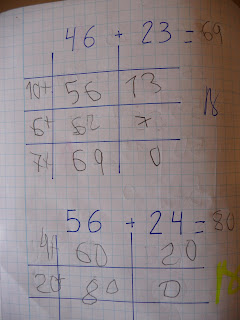




Ví la noticia en TV. Busqué en Internet y leí un par de artículos. Por fín le he encontrado.
ResponderEliminarSencillamente maravilloso. Enseñar a los críos lo que nuestras cabezas hacen. O ¿no hacemos nosotros así las cuentas? Ya habrá tiempo de explicarles Leyes Distributivas y otras.
Tengo un hijo de 5 años, recien cumplidos, y acabo de encontrar en este método un nuevo "juego" para compartir con él.
Gracias y ánimo.
Gracias a ti. Confío en que tu hijo no se tenga que tragar los rollos de las llevadas, las traídas y todos los inconvenientes de unos formatos absolutamente "gagás".
ResponderEliminarGuau, Como Hacia Yo Las Cuentas
ResponderEliminar